[DirectX 12를 이용한 3D 게임 프로그래밍 :: Chapter 01] 벡터 대수

1.1 벡터 

 

벡터(Vector, 방향량) : 크기와 방향을 모두 가진 수량(quantity)을 가리키는 말. 힘이나 변위, 속도(velocity)를 나타내는 데 쓰인다.

 

- 위치를 바꾸어도 벡터의 크기와 방향은 변하지 않는다.

- 두 벡터가 길이가 같고 방향이 같다면, 오직 그럴 때만 상등(equal)이다.

 

1.1.1 벡터와 좌표계

 

같은 벡터 v라도 기준계가 다르면 그 좌표 표현이 달라진다.

어떤 벡터를 좌표로 규정하거나 식별할 때 그 좌표가 절대적인 수치들이 아니라 항상 어떤 기준계에 상대적인 수치들임을 뜻한다.

 

1.1.2 왼손잡이 좌표계 vs 오른손잡이 좌표계

 

왼손 좌표계 : Direct3D, 언리얼, 유니티

오른손 좌표계 : 블랜더 3D

※ 좌표계에 대한 더 많은 이야기 : [게임 수학] 3차원 공간 맛보기 (velog.io)

[게임 수학] 3차원 공간 맛보기

 

1.2 길이와 단위벡터

 

벡터의 크기(길이) : 이중 수직선(||u||)로 표기한다. 벡터  u의 크기는 피타고라스의 정리를 두 번 적용해서 계산할 수 있다.

벡터 크기(길이) 공식

단위벡터(unit vector) : 크기가 1인 벡터.

정규화(normalization) : 임의의 벡터를 단위 벡터로 만드는 것.

정규화 공식

 

1.3 내적

 

점곱(dot product) / 내적(inner product) : 스칼라 값을 내는 벡터 곱셈의 일종. 결과가 스칼라 값이여서 스칼라 곱(scalar product)이라고도 한다.

 

벡터 u = (ux, uy, uz), 벡터 v = (vx, vy, vz)일때,

u와 v의 내적

으로, 대응되는 성분들의 곱의 합이다. 코사인 법칙을 사용하면

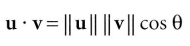
여기서 θ는 벡터 u와 v 사이의 각도(0 ≤ θ ≤ π)이다.

 

1.u · v = 0이면 u⟂v이다(두 벡터는 직교).

2.u · v > 0이면 두 벡터 사이의 각도 θ는 90°보다 작다(두 벡터는 예각).

3.u · v < 0이면 두 벡터 사이의 각도 θ는 90°보다 크다(두 벡터는 둔각).

 

1.3.1 직교화

 

정규직교(orthonormal) : 벡터들의 집합 {v0, ..., vn-1}이 주어졌을 때, 모든 벡터가 단위길이이고, 서로 직교일 때(즉, 집합의모든 벡터가 다른 모든 벡터와 수직일 때)의 벡터 집합.

 

직교화(orthonormalization) : 정규직교벡터 집합으로 만드는 것.

 

- 2차원 벡터 집합 {v0, v1}을 정규직교 집합 {w0, w1}로 만들기

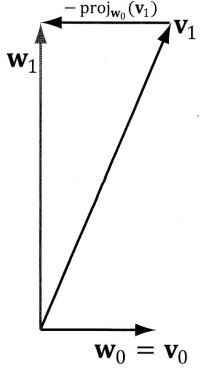
v1에서 w0의 방향으로 작용하는 부분을 빼는 것. w1 = v1 - projw0(v1)

 

- 3차원 벡터 집합 {v0, v1, v2}을 정규직교 집합{w0, w1, w2}로 만들기

2차원과 같은 방식으로 w2 = v2 - projw0(v2) - projw1(v2)

 

이를 일반화해서, n개의 벡터들의 집합 {v0, ..., vn-1}을 직교화는 그람-슈미트 직교화(Gram-Schmidt Orthogonalization)라는 공정을 적용한다.

그람-슈미트 직교화

1. 입력 집합에서 벡터 vi 택하기.

2. 이미 직교 벡터 집합에 들어있는 다른 벡터들 (w0, w1, ..., wi-1)과 빼서 직교가 되게 만들기.

3. 반복

 

1.4 외적

 

가위곱(cross product) / 외적(outer product) : 내적과 달리 결과가 벡터이다. 3차원 벡터에만 정의. 두 3차원 벡터 u와 v의 외적을 취하면 u와 v 모두에 직교인 또 다른 벡터 w가 나온다.

 

- 교환 법칙이 성립되지 않음.(u × v = -v × u)

- 왼손 엄지 법칙 : 왼손 좌표계라면 u와 v의 외적은 왼손의 엄지방향 (빵야같은 손짓인듯?)

 

벡터 u = (ux, uy, uz)이고 v = (vx, vy, vz)일 때,

w = u × v = (uyvz - uzvy, uzvx - uxvz, uxvy - uyvx)

 

1.4.1 2차원 유사 외적

 

2차원에선 외적이 적용되지 않지만, 하나의 2차원 벡터 u = (ux, uy)가 주어졌을 때, u에 수직인 벡터 v를 구하는 것은 가능.

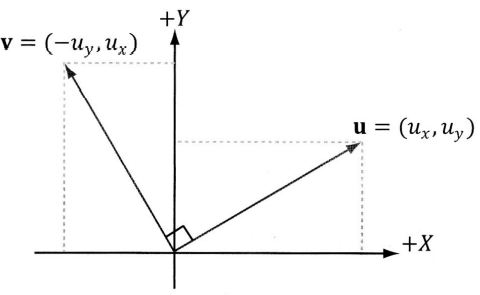
- 증명 : 내적 각도가 수직(90도)이므로 u · v = 0

u · v = (ux, uy) · (-uy, ux) = -uxuy + uyux = 0

u⟂v이다. u · v = uxuy + uy(-ux) = 0도 성립하므로 u⟂-v도 성립.

 

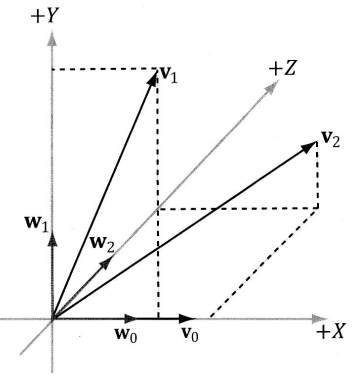
1.4.2 외적을 이용한 직교화

 

그람-슈미트 직교화 공정을 이용해서 벡터 집합을 직교화하는 방법을 1.3.1에서 배웠었다. 3차원의 경우 정규직교에 아주 가깝지만 수치 정밀도 오차 누적 때문에 완전한 정규직교는 아닌 벡터 집합 {v0, v1, v2}를 외적을 이요해서 직교화하는 또다른 공정이 존재한다.

외적을 이용한 3차원 직교화

1.5 점(위치 벡터)

 

위치 벡터(position vector) : 특정 좌표계를 기준으로 표준 위치에 있는 벡터를 3차원 공간의 한 위치를 나타내는 데 쓰임.

벡터의 머리 끝의 좌표가 벡터의 위치이다.

위치 벡터

(a) : 두 위치벡터의 차 q - p는 p에서 q로 가는 벡터이다.

(b) : 두 위치벡터의 합 q + p는 p의 위치를 v만큼 옮겨서 얻는 위치벡터 q이다.

---

요약